|
1-8. 진자의 운동 (물리진자, 비틀림진자)
(Last Updated 2004/3/31) 1. 실험목적
여러가지 물체의 진자운동과 비틀림 진동을 컴퓨터 인터페이스를 통해 관찰하고 그 주기를 측정하여 이론값과 일치하는가를 확인한다.
2. 이 론
A. 물리진자(Physical Pendulum)
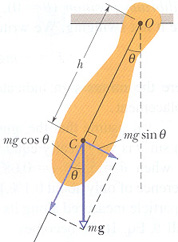
[그림1] 물리진자 |
[그림1]과 같이 실제 세계에서의 물리진자에 대해 물체를 강체라고 가정할때 질량중심을 C, 고정점을 O, 질량중심과 고정점 사이의 거리를 h 라하면 평형상태(θ=0 일때) 에서는 고정점 O에 대해 점 C는 수직으로 매달리게 된다.
그런데, 물체에 각도 θ만큼 변위가 가해지면 중력 mg 에의해 물체에는 복원력 토오크가 생기고
τ= -h(mg sinθ) ----------(1)
이다. 여기서 - 부호는 복원력 토오크임을 나타내고 각도 θ를 0 으로 줄이기 위해 작용한다. τ= Iα(I는 관성모멘트, α는 각가속도) 이므로
τ= I d2Θ/dt2 = -mgh sinΘ---(2)
가 된다. 여기서 진폭이 아주 작을때, (Θ≪ 1 ; 5°이하) sinΘ≒Θ이고
d2Θ/dt2 +(mgh/I )Θ= 0 -------------(3)
이므로 이 미분방정식의 해는 |
Θ= Acosωt + Bsinωt (ω=(mgh/I)1/2 )----(4)
이다. t=0 일때 초기각은 Θ0 , dΘ/dt=0 이라 하면, A=Θ0 , B=0 이므로
Θ= Θ0cosωt ---------------(5)
ω=2πf=2πT-1 이므로 이 물리진자의 주기는
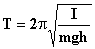 -----------(6) -----------(6)
여기서 I 는 고정점(O)을 지나는 수직축에 대한 물체의 관성모멘트를 나타내고, h는 질량중심과 고정점사이의 거리를 나타낸다.
만약 고정점을 질량중심으로 잡는다면 물리진자는 진동하지 않는데, 위의 식에서 보는 바와같이 h →0 이면 주기 T →∞가 되어 물체는 변위가 가해져도 진동하지 않음을 나타내고 있다. 길이 L인 실 끝에 질량(m)이 매달려 있는 단진자의 경우는 I = mL2 , h = L 인 경우 이므로 (6)식에서 T = 2π(L/g)1/2 임을 알수있다.
우리는 이 실험에서 물리진자를 좀더 단순화하여 균일한 밀도, 일정한 두께의 막대기와 원반시료를 사용하여 물리진자의 운동을 알아볼 것이다.
(1) 막대진자
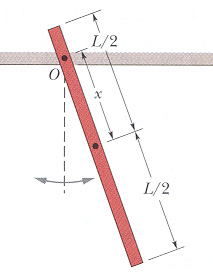
[그림2] 막대진자 |
[그림2]와 같이 길이 L인 막대의 한쪽(O점)을 고정하고 일정한 변이를 주어 물체를 진동시킬때 진동주기를 구해보자.
막대의 질량을 m 이라 하면 고정점 O에 대한 막대의 관성모멘트는
I = ∫r 2 dm = ρ∫r 2 dr (ρ:선밀도) = 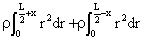
위 적분을 계산하거나 또는 평행축 정리에 의해
I = I O = I c.m + mh 2 = 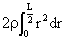 + mx 2 = 1/12 mL 2 + mx 2 --------(7)
이므로 식(6) 으로부터 미소진동 일때 진자의 주기는 |
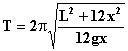 ------(8)
이다. 즉, 이것은 길이가 (L2+12x2)/(12x) 인 단진자의 운동으로 생각할 수 있다.
(2) 원반진자
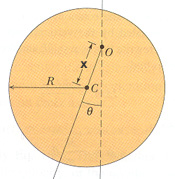
[그림3] 원반진자 |
[그림3]과 같이 중심 C로 부터 x 만큼 떨어진 지점 O를 고정하고 변위를 가할때 진동하는 원반 물리진자에 대해 생각해 보자.
원반의 중심에 대한 관성모멘트 I c.m = 1/2 mR2 (R:반지름, m:원반질량) 이므로, 평행축정리에 의해
I = I O = I c.m + mh2 = 1/2 mR2 + mx2
이다. 그러므로 식(6) 으로부터 미소진동 일때 진자의 주기는
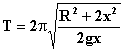 ------(9) |
이것은 길이가 (R2+2x2)/(2x) 인 단진자의 운동으로 생각할 수 있다.
B. 비틀림진자(Torsion Pendulum)
[그림4]와 같이 원판의 질량중심을 철사로 매달고 철사가 지지대의 끝에 단단히 고정되어 있을때 원판은 평형위치(Reference line)에서 정지해 있다.
원판이 축을 중심으로 θm 만큼 변위가 가해지면 비틀린 철사에는 복원 회전력이 생기고 이 복원회전력은 비틀린 각변위, θ에 비례하므로
τ = -κθ-------(10)
이다. 여기서 κ는 철사의 특성(길이, 직경 등)에 관계되는 상수이며 비틀림상수라 한다.
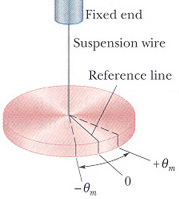
[그림4] 비틀림 진자 |
이 계에 대한 운동방정식은 τ = Iα = Id2Θ/dt2 이므로
-κθ = I d2Θ/dt2d2Θ/dt2 = -(κ/I)θ---(11)
이다. 이것은 스프링에 매달린 질량의 단순조화운동과 비슷하며 직선변위 x ⇒ θ, 질량 m ⇒ I 를 힘상수 k ⇒ κ로 대치한 것과 같다. 방정식 (11)의 해는 t=0 일때 초기각을 Θm 이라하면
Θ= Θmcosωt -----------(12)
이고, ω = 2πf = 2πT-1 이므로 이 비틀림 진자의 주기 T는
T = 2π(I/κ)1/2 ---------(13) |
이다. 검류계등 많은 실험기구들이 비틀림 진동과 관계가 있으며 만유인력 상수(G)를 측정하기 위한 카벤디쉬의 천칭 도 비틀림 진자를 이용한 것이므로 매우 중요하다.
3. 실험기구 및 장치
(1) 컴퓨터 및 인터페이스 장치
(2) 회전센서(Rotary Motion Sensor; 3단 도르래 직경 = 각각 10, 29, 48mm)
(3) 막대진자 (2종, 길이=50cm, 직경=6mm), 원반진자(r=10cm)
(4) A 베이스 및 지지막대(60cm)
(5) 자(30cm) 또는 줄자
(6) 비틀림 진자용 철사 3종(길이= 45.7cm, 두께= 0.8mm, 1.2mm, 1.6mm)
(7) 힘센서(Force Sensor)
(8) 원반디스크 (질량=124g, 반경=4.7cm)
(9) 철사 클램프 (상,하 2종)
(10) 실, 가위
4. 실험 방법
A. 물리진자

[그림5] 센서의 셋업 |
(1) 회전센서의 폰 플러그 노랑색, 흑색을 순서대로 디지탈 채널1, 2에 연결하고, [그림6]과 같이 회전센서를 스탠드에 고정한다.
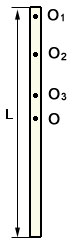
(2) 막대진자에는 구멍이 여러개 뚫려 있는데, 먼저 막대의 중심(질량중심)으로부터 각 구멍의 중심까지의 거리를 자로 측정하여 기록해둔다.
(3) 회전센서의 중심에 있는 나사를 이용하여 맨 끝의 구멍 O1 을 고정한다. |

[그림6] 물리진자 |
 |
(4) 데이터스튜디오 프로그램을 실행하고 회전센서(Rotary Motion Sensor)를 디지털 채널1로 끌어다 놓으면 [그림5]와 같이 된다.
(5) 센서를 더블클릭-General 탭의 Sample Rate은 20Hz, Measurement 탭은 각위치(Angular Position; rad)를 선택, Rotary Motion Sensor탭의 Division/Rotation(1회전당 분해능)은 1440을 선택-확인 한다.
(6) 시간에 따른 회전각의 변화를 보기위해 아이콘을 회전센서아이콘 으로 끌어가서 그래프 윈도우를 띄운다. 여기서 필요하다면 각속도, 각가속도 등도 선택할 수 있다.
(7) 진자막대를 대략 5° 각도 이내로 진폭을 주어 진동시키고 상단의 시작버튼  을 눌러 데이타저장을 시작한다. (회전센서는 초기각위치를 0 으로 설정하므로 정지상태에서 데이타저장을 시작한 다음, 진폭을 주어 진동시키면 수직 평형위치 0 점에 대한 진동그래프를 얻을수 있다.) 을 눌러 데이타저장을 시작한다. (회전센서는 초기각위치를 0 으로 설정하므로 정지상태에서 데이타저장을 시작한 다음, 진폭을 주어 진동시키면 수직 평형위치 0 점에 대한 진동그래프를 얻을수 있다.) | (8) 3~5초 정도 데이타를 저장한 다음 정지  하고 그래프 윈도우에서 오토스케일 하고 그래프 윈도우에서 오토스케일  버튼을 눌러서 크기를 보기좋게 조절한다. 버튼을 눌러서 크기를 보기좋게 조절한다.
(9) 실험으로부터 얻은 데이터 곡선에서 스마트커서  버튼을 선택하여 진자의 진동주기를 구한다. (그래프를 충분히 확대하고 소수 3째 자리까지 구하되 각위치가 0 이 되는 주기 시간간격을 측정하는것이 용이할 것이다) 원래는 각위치가 0 이되는 시간은 각위치가 0 에 가까운 ±두 점을 비례식을 이용해 계산해야 겠지만 그래프를 확대하여 스마트커서를 사용하면 이미 컴퓨터가 비례식에 의해 계산하여 위치를 나타내므로 이 단순한 작업들은 생략한다. 각진폭이 5° 이내 즉, 0.087(rad) 이내에 있는가를 확인해보고 진폭이 너무 크거나 너무 작지 않도록 데이타를 저장한다. 버튼을 선택하여 진자의 진동주기를 구한다. (그래프를 충분히 확대하고 소수 3째 자리까지 구하되 각위치가 0 이 되는 주기 시간간격을 측정하는것이 용이할 것이다) 원래는 각위치가 0 이되는 시간은 각위치가 0 에 가까운 ±두 점을 비례식을 이용해 계산해야 겠지만 그래프를 확대하여 스마트커서를 사용하면 이미 컴퓨터가 비례식에 의해 계산하여 위치를 나타내므로 이 단순한 작업들은 생략한다. 각진폭이 5° 이내 즉, 0.087(rad) 이내에 있는가를 확인해보고 진폭이 너무 크거나 너무 작지 않도록 데이타를 저장한다.
(10) (8)식 으로부터 계산된 이론치(T)와 측정한 진자의 진동주기(Te)를 기록하고 오차(%)를 계산해본다. 데이터그래프도 보고서에 첨부하도록 한다.
[표1]
|
고정점 |
측정값 |
이론값(T) |
오차(%) |
|
T1e |
T2e |
T3e |
평균(Te) |
|
O1 |
|
|
|
|
|
|
|
O2 |
|
|
|
|
|
|
|
O3 |
|
|
|
|
|
|
(11) 시료막대를 다른것으로 바꾸어 위의 과정 (7)~(10)을 반복하고 데이터 [표1]을 기록한다. 질량이 다른 똑같은 부피의 막대진자는 같은 주기를 갖는가? 각각의 고정점에 대해 진자의 주기 T1,T2,T3 의 크기를 순서대로 나열하면? 주기 T를 x의 함수로 그려보자.
| [질문] 위의 두 막대진자에서 같은 고정점 거리에 있는 진자의 주기를 비교하여 보자. 진자의 주기는 질량에 관계있는가? 일반적으로 진자의 운동은 단순조화 운동이 아님을 보여라. |
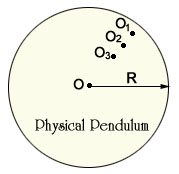
[그림7] 원반진자 |
(13) 원반진자: 원반상의 바깥쪽 구멍 O1 으로부터 안쪽으로 고정점을 이동해가며 진자의 운동을 관찰하고 위와같이 [표1]을 기록해보자.
(14) 막대진자나 원반진자의 중심(질량중심)을 센서에 고정하고 물체에 진폭을 가하면 어떻게 되는가? 주기는 어떠한가? (무한대? 또는 영?)
(15) 막대진자와 마찬가지로 고정점의 위치 x 의 변화에 따른 진자의 주기곡선을 그려보라. 얼핏보면 고정점의 위치가 바깥쪽으로 이동할수록 진자의 길이가 길어져 주기가 느려질것 같지만 결과는 어떠한가? |
B. 비틀림 진자

[그림8] 센서의 셋업 |
(1) 앞의 실험데이터를 저장해주고 File => New Activity 하여 왼쪽 그림과 같이 센서를 다시 설정해주고 [그림9]와 같이 실험장치를 꾸며보자. A 베이스에 지지막대를 세우고 하단클램프를 끼운다음, 상단에 회전센서를 고정한다.
(2) 철사(직경=0.8mm)를 상단클램프에 [그림9]와 같이 고정하고 회전센서 하단에 슬럿 홈에 맞추어 끼우고 하단 클램프에 나사로 고정한다. 이때 철사가 휘어지거나 변형되지 않도록 상하단 길이를 잘 조절해 주고 너무 꽉 조이지 않도록한다. |
|
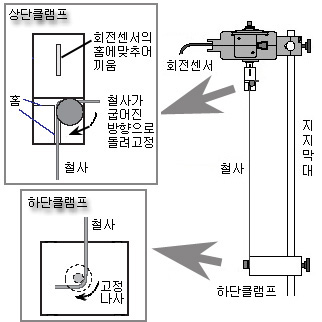
[그림9] 비틀림 장치의 셋업
|

[그림10] 비틀림 상수 측정 |
(3) 비틀림상수(κ) 의 측정
① 먼저 철사에 대한 비틀림상수를 측정해보자. 힘센서 아이콘을 더블클릭하여 샘플링속도를 20Hz 로 설정하고 영점(Tare)버튼을 눌러준다.
[참고]
(1) 회전센서의 방향구분: PASCO라고 써진 부분의 반대쪽에 3단도르래가 달리고 이 도르래가 우측으로 돌아가면 +, 좌측은 - 로 표시된다.
(2) 토오크를 그래프윈도우에 직접 표시하려면 계산기윈도우  를 활용하면 된다. 힘센서는 당겨질 때 -로 표시되므로 torque = -r * force 형식으로 정의해주면 1사분면에 보기좋게 표시될 것이다. 를 활용하면 된다. 힘센서는 당겨질 때 -로 표시되므로 torque = -r * force 형식으로 정의해주면 1사분면에 보기좋게 표시될 것이다.
(3) 철사를 갈아주기가 번거로우므로 각각의 철사에 대한 비틀림상수측정 => 진동주기측정 으로 실험을 진행하자. 비틀림상수 측정 설정파일과 진동측정 설정파일을 적당한이름으로 저장해주고 파일 불러오기로 실험하면 편리할것이다. |
(4) 원반질량에 의한 비틀림진동
① 이제, 실을 도르래에 감아놓고 비틀림진자의 운동으로부터 주기를 구해보자. 원반을 회전센서 위에 올려놓고(가운데 사각홈을 맞추어 끼운다) 나사로 조인다.
④ 오토스케일 버튼  을 누르고 각 위치의 최대 또는 최소 사이의 시간간격을 알아보기 위해 스마트커서 을 누르고 각 위치의 최대 또는 최소 사이의 시간간격을 알아보기 위해 스마트커서  를 선택하여 진자의 진동주기 값을 5개정도 측정한다.(소수 4째자리 까지 측정-그래프를 최대한 확대하는 것이 유리. 를 선택하여 진자의 진동주기 값을 5개정도 측정한다.(소수 4째자리 까지 측정-그래프를 최대한 확대하는 것이 유리.
[참고] 기준점에 스마트커서  표시를 놓고 그 부근에서 커서가 삼각형과 손 표시 표시를 놓고 그 부근에서 커서가 삼각형과 손 표시  가 나타날 때 클릭-드래그하면 시간간격이 표시된다) 평균하여 주어진 철사에 대한 비틀림 진동주기 값을 기록하고, 디스크의 질량과 반경 측정에 의한 관성모멘트 이론값 I 를 구하고 T = 2π(I/κ)1/2 로부터 계산된 이론치와 측정한 진자의 진동주기 사이의 오차(%)를 계산해본다. 가 나타날 때 클릭-드래그하면 시간간격이 표시된다) 평균하여 주어진 철사에 대한 비틀림 진동주기 값을 기록하고, 디스크의 질량과 반경 측정에 의한 관성모멘트 이론값 I 를 구하고 T = 2π(I/κ)1/2 로부터 계산된 이론치와 측정한 진자의 진동주기 사이의 오차(%)를 계산해본다.
| ⑤ 두께= 1.2mm, 1.6mm 철사 중 1개를 선택하여 위의 실험을 되풀이 해보고 주기와 진폭 그리고 철사 두께와 감쇄진동 사이의 관계를 설명해보자. (너무 빨리 진동하면 샘플링속도를 500Hz 정도로 높여준다)
5. 참 고
(1) Torsion Pendulum (PDF 파일)
(2) 일반적 진자의 주기공식 / 세상에서 가장빠른 진자
(3) 만유인력상수(G) 측정실험 (카벤디쉬 실험)
|
 실험실소개
실험실소개
 실험실위치
실험실위치
 오시는길
오시는길