|
2-3. RC 직류회로
(Last Updated 2010/8/25)
1. 실험목적
축전기(Capacitor) 에 직류전압이 가해질 때 충,방전되는 전압 및 전류의 시간적 변화를 그래프로 관찰하고, 정전용량, C 값이 실험값과 일치하는가를 확인한다.
2. 원 리
2-1. 축전기의 충전
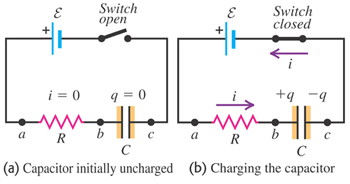
[그림1] RC 회로의 충전 |
[그림1]은 축전기를 충전하기 위해 단순히 저항과 축전기를 직렬로 연결한 'R-C 직렬회로' 이다.
우리는 배터리(또는 전원장치)가 일정한 기전력 ε (= V0)를 갖고 내부저항은 0이라 가정하고 모든 연결도선의 저항을 무시한다.
축전기가 충전되어 있지 않을 때 [그림1(a)], 초기시간, t=0 에서 스위치를 닫으면 [그림1(b)]와같이 회로를 따라 전류가 흐르고 축전기에 충전이 시작된다. 실제로 전류는 회로내의 모든 도체부분에서 같은 순간에 시작되고 크기는 같다. |
축전기는 처음에 충전되어있지 않기 때문에 축전기 양단의 전위차, vbc 는 t=0 일 때 영이되고 이때 키르히호프의 폐회로 법칙(Kirchhoff's loop law) 으로부터 저항 R 양단의 전위차, vab 는 배터리 기전력 V0와 같다. 저항을 통해 흐르는 초기(t=0) 전류, I0 는 오옴의 법칙(Ohm's Law)에 의해 I0 = vab/R = ε/R 으로 주어진다. 축전기가 충전됨에 따라 vbc 는 증가하고 전류가 감소함에 따라 vab 는 감소하는데 이 두전압의 합은 V0와 같아야 할 것이다. 충분한 시간이 흐르면 축전기는 완전히 충전되고 전류는 0, vab 는 0 이 된다. 즉, vab= iR, vbc = q/C 이므로 키르히호프의 폐회로 법칙(Kirchhoff's loop law) 으로부터
V0 -iR - q/C = 0 ------(1)이된다. 식을 변형하면
i = V0/R - q/RC 이되고, i = dq/dt 이므로
R(dq/dt) + q/C = V0 이 미분방정식의 해는
q = CV0(1 -e-t/τ) = Qf(1 -e-t/τ) --------(2)
회로전류는
i = dq/dt = (V0/R)e-t/τ = I0 e-t/τ--------(3)
이다. 여기서 Qf = CV0 는 축전기에 충전되는 최대 전하량이며 τ= RC 로 정의한다. 여기서 τ는 시정수(time constant) 또는 지체시간(relaxation time) 이라 부른다.
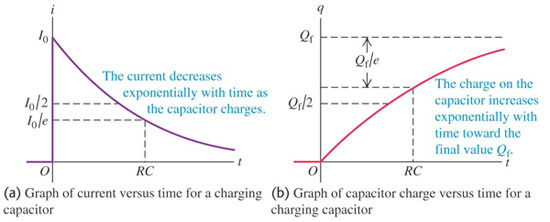 [그림2] 축전기 충전시 시간에 따른 회로전류와 전하량 변화 [그림2] 축전기 충전시 시간에 따른 회로전류와 전하량 변화
충전전하와 전류는 시간의 지수함수로 나타난다. 즉, 회로전류는 아주 짧은 시간동안 흐르는데 축전지는 지수적으로 충전되고 정상상태에 도달하며 전류가 흐르지 않는다. 축전지에 전하가 절반이 충전되었을 때, 시정수는
t1/2 = τln2, C = t1/2/(R ln2) ------(4)
이 된다. 시정수 τ가 작으면 축전기는 빨리 충전되고 크면 서서히 충전됨을 알 수 있다. 만일 저항이 작다면 전류는 흐르기 쉬워질 것이고 축전기는 더욱 빨리 충전될 것이다.
2-2. 축전기의 방전
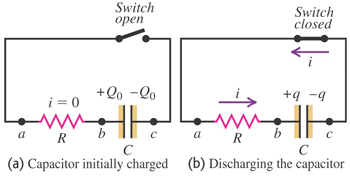
[그림3] RC 회로의 방전 |
우리는 이제 전하, Q0 를 갖는 축전기에 대해 생각해 보자.
R-C 회로로 부터 배터리(또는 전원장치)를 제거하고 스위치를 연결한다. [그림3(a)] 초기시간, t=0 에서 스위치를 닫으면(이때 초기전하, q=Q0 ) [그림3(b)]와 같이 축전기는 저항을 통해 방전을 시작하고 결국 0으로 감소 할 것이다. 전류 i와 전하량 q 는 시간에 따른 변량이라고 하면 키르히호프의 폐회로 법칙(Kirchhoff's loop law)에 의해 (위의 식(1)에서 V0=0 인 경우와 같으므로)
|
i = dq/dt = -q/RC ---------(4)
이다. 여기서 전류를 음(-)으로 잡은 이유는 [그림3(b)]와 같이 축전기 왼쪽 극판을 떠나는 양전하 q가 전류의 방향과 반대이기 때문이다. 이식의 양면을 적분하면
q = Q0 e-t/τ -------------(5)
이 되고 전류는 이식을 다시 t 로 미분하여
i = dq/dt = -(Q0/RC)e-t/RC = I0 e-t/τ --------(6)
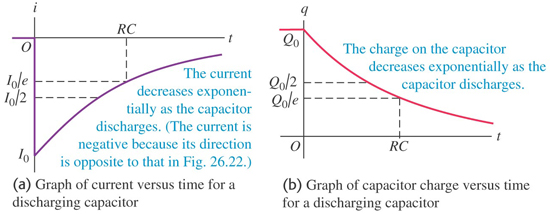
[그림4] 축전기 방전시 시간에 따른 회로전류와 전하량 변화
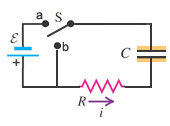
[그림5] RC회로의 충방전 |
우리는 그림1 과 3을 연속동작으로 수행할 수 있는 회로를 [그림5]와 같이 나타낼 수 있다. 또한 축전기의 전하량은 q = CVc 이므로 위의식 (2), (5)는 축전기 양단의 전압 Vc 로 바꾸어 다음과 같이 나타낼 수 있다.
Vc = V0( 1 -e-t/τ) [충전]------(7)
Vc = V0 e-t/τ [방전]------(8) | |
우리는 이 실험에서 축전기(콘덴서 사용) 양단의 전압변화를 초당 최대 10만개의 전압값을 읽어들일 수 있는 PC인터페이스를 이용하여 정밀하게 측정하고 이론식과 일치하는가를 확인할 것이다.
또한 축전기 양단 전압의 변화 그래프에서 충전(또는 방전)되는 시간의 하프타임(t1/2 )을 측정하고 식(4)를 이용하여 실제 콘덴서의 충전용량 C 를 계산할 것이다. 전류(i)나 전하량(q) 변화 곡선은 전압변화 곡선의 미분형이거나 파라미터를 적당히 조절하면 구할 수 있으므로 전압변화를 측정하면 우리는 실제로 다른 데이터들을 모두 구한 것과 같다.
많은 중요한 장치들이 충방전을 반복하는 축전기를 회로에 포함하고 있는데, 의학적 응용으로는 심장 맥박조정기, 교통 신호등의 점멸, 자동차의 방향지시등, 전자 플레시 모듈 등 다양한 방면에 사용되고 있다. 그러한 회로내에서 무슨일이 일어나는가를 이해하는 것은 매우 중요한 일이다.
3. 실험기구
4. 실험방법

[그림5] 센서의 셋업 |
(1) 데이터스튜디오 프로그램을 실행하고 [그림5]와 같이 채널A에는 전압센서, 채널B에는 파워앰프를 설정하고 실제로 도 센서를 연결해 준다.
(2) 신호발생기의 출력 설정은 4.00V, 1.2Hz,  양의구형파(positive squire Wave), Auto(디폴트값)로 설정하고 파워앰프 전원을 켠다. 양의구형파(positive squire Wave), Auto(디폴트값)로 설정하고 파워앰프 전원을 켠다. |
[참고]
여기서 1.2Hz 양의구형파란 무엇일까? 이것은 초당 1.2번  사각파형의 전원이 공급된다는 의미이므로 사각파형의 주기가 0.83초(=1/1.2초) 이고 실제로 사각파형 전원은 0.415초 동안 DC4V 가 걸리고 나머지 0.415초 동안은 0V로 꺼지며 이러한 전원 공급이 반복적으로 가해진다는 것을 의미한다. 사각파형의 전원이 공급된다는 의미이므로 사각파형의 주기가 0.83초(=1/1.2초) 이고 실제로 사각파형 전원은 0.415초 동안 DC4V 가 걸리고 나머지 0.415초 동안은 0V로 꺼지며 이러한 전원 공급이 반복적으로 가해진다는 것을 의미한다. |

[그림6] RC 회로의 연결 |
(3) 샘플링 옵션  => Automatic Stop 에서 Time은 2.00 seconds(2초동안 실험)로 쓰고 확인 한다. 전압센서 아이콘을 더블클릭하여 샘플링속도(Sample Rate)는 1000Hz로설정한다. => Automatic Stop 에서 Time은 2.00 seconds(2초동안 실험)로 쓰고 확인 한다. 전압센서 아이콘을 더블클릭하여 샘플링속도(Sample Rate)는 1000Hz로설정한다.
(4) 회로판의 인덕터 코일 양단을 리드선으로 연결(인덕터 점프)하고 파워앰프의 전원 출력단자를 100Ω,330㎌ 하단부의 파란색 단자에 리드선으로 연결하여 R(100Ω)-C(330㎌) 직렬회로가 되도록 구성한다.
(5) 전압센서A 를 330㎌ 콘덴서(표면에 - 극성이 화살표로 표시되어 있으므로 구분하여 극성에 맞게 연결!) 양단에 연결한다.
(6)  아이콘을 좌상단(Data영역) 채널A, Voltage로 끌어가서 v-t(콘덴서 양단전압) 그래프윈도우를 띄운다. 아이콘을 좌상단(Data영역) 채널A, Voltage로 끌어가서 v-t(콘덴서 양단전압) 그래프윈도우를 띄운다.
(7) 담당조교에게 배선상태를 확인받고  를 누른다. 데이타 저장을 시작하면 2초간 데이타 저장후 자동으로 종료된다. (시간 미지정시 데이터가 너무 많이 저장됨) 를 누른다. 데이타 저장을 시작하면 2초간 데이타 저장후 자동으로 종료된다. (시간 미지정시 데이터가 너무 많이 저장됨) |
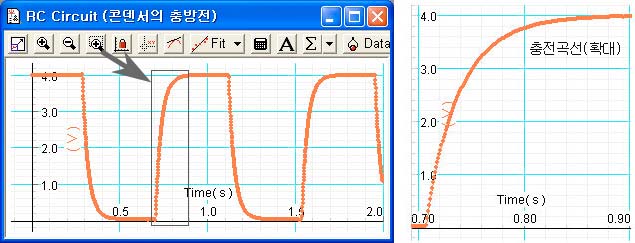
(8) 그래프 윈도우에서 오토스케일(Autoscale)  을 누르고 콘덴서 및 저항 양단의 전압변화를 관찰한다. ([그림7]는 실험에서 실제로 나타나는 곡선. 우측은 확대) 을 누르고 콘덴서 및 저항 양단의 전압변화를 관찰한다. ([그림7]는 실험에서 실제로 나타나는 곡선. 우측은 확대)
 |
|
[그림7] 콘덴서의 충,방전 곡선 |
(9) 부분확대 아이콘  을 누르고 그래프에서 자세히 보기 원하는 전압상승 영역을 확대한다. 을 누르고 그래프에서 자세히 보기 원하는 전압상승 영역을 확대한다.
(10) 원하는 위치의 값을 정밀하게 읽기위해 그래프를 모니터에서 최대한 확대하고 스마트커서(Smart Cursor)  를 선택하고 커서를 전압이 상승되는 지점에 위치시켜서 시간값(t0)을 기록한다. 를 선택하고 커서를 전압이 상승되는 지점에 위치시켜서 시간값(t0)을 기록한다.
(11) 스마트커서를 최대전압의 1/2 지점인 2.00V 되는 지점에 위치시키고 그때의 시간값 t1/2' 을 기록한다. (더욱 정확한 값을 얻기 위해 필요하다면 샘플링의 속도를 5000Hz 정도까지 높일 수 있다. 그래프 윈도우의 시간축 크기는 ms 단위로 잡고, 시간값은 데이터테이블을 이용하여 소수 6째자리 까지 찾을 수 있다.)
(12) 두 시간사이의 차이 t1/2 (=t1/2'-t0)를 구하고, t1/2= τln2 = RC ln2 관계로부터 C 값을 구한다.
(13) 방전 곡선에서도 위와같이 계산하여 보자. 콘덴서가 충전될때와 방전될때 시상수는 같은가?
[질문]
전원장치 역할을 하는 파워앰프 전원이 꺼지는 경우(0V), 왜 방전되는 곡선이 나타난 것일까? 파워앰프가 0V인 경우, 파워앰프는 회로에서 어떻게 작동하고 있는 것일까? |
(14) 실험에서 구한 C 값을 용량값과 비교하여 오차(%)를 계산해보라. 이 값은 오차허용 범위인 20% 이내에 있는가? (콘덴서의 공칭값-표면에 표기된 값; ±20% 오차를 허용-을 참값으로 사용하고 만약, LCR 메타가 있다면 콘덴서의 C 값을 측정하여 이 값에 대한 오차를 계산한다) 또 충방전 전류에 대한 데이터 그래프를 얻어보고 회로전류의 흐름 양상을 설명하여 보자.(그래프셋팅-Layout탭-Layering-Overlay Graphs를 이용하여 여러그래프 동시 표시가능)
(15) [키르히호프의 법칙] 전압센서를 2개 사용하여 저항과 콘덴서 양단의 전압을 동시에 측정하고 얻은 데이터를 이용하여 임의의 시간에 대해 키르히호프의 법칙을 만족하는가를 알아보자. ☞ 채널A와 C의 전압 그래프를 합한 그래프 V는 전원입력과 같은가를 확인. (V = VR+ VC)
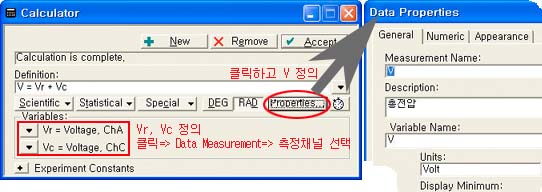 [그림8] 계산기윈도우의 활용 [그림8] 계산기윈도우의 활용
ⓐ 먼저 계산기 를 띄우고 [그림8]과 같이 Definition 란에 V = Vr+ Vc를 입력한 다음, Properties를 클릭하여 V를 정의(그림우측-다른 것은 디폴트값)해주고 Variables 란에서 위 그림과 같이 표시되도록 Vr , Vc를 정의해 준다. 그러면 데이터 영역(화면 좌상단)에 V = Vr+ Vc 가 표시될것이다. 를 띄우고 [그림8]과 같이 Definition 란에 V = Vr+ Vc를 입력한 다음, Properties를 클릭하여 V를 정의(그림우측-다른 것은 디폴트값)해주고 Variables 란에서 위 그림과 같이 표시되도록 Vr , Vc를 정의해 준다. 그러면 데이터 영역(화면 좌상단)에 V = Vr+ Vc 가 표시될것이다.
ⓑ  아이콘을 데이터 영역 V = Vr+ Vc 으로 끌어가서 그래프(V-t)를 띄우고 실험을 수행하여 보자. 아이콘을 데이터 영역 V = Vr+ Vc 으로 끌어가서 그래프(V-t)를 띄우고 실험을 수행하여 보자.
ⓒ 측정된 V값과 신호발생기의 출력전압 값을 비교하여 보자. 키르히호프의 법칙은 성립하는가?
|
(16) 100㎌ 콘덴서에 대해서도 위의 과정을 반복하여 충방전 양상을 실험하고 전기용량 C값을 구한다.
5. 참 고
(1) RC 직류회로 (pdf 파일)
|
 실험실소개
실험실소개
 실험실위치
실험실위치
 오시는길
오시는길