|
|
|
|
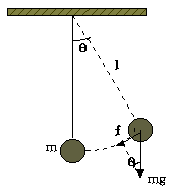
Ref 1. 일반각에 대한 단진자의 주기공식 미소진동이 아닌 일반각(초기진폭= q0)에 대한 단진자(Simple Pendulum)의 주기공식은 다음과 같음을 보이자. 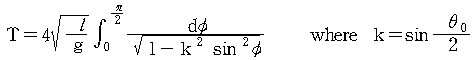
초기위치 q = q0 에서 u=0 이므로 c= -(g/ℓ)cosq0이므로 (3)식은 여기서 q = q0 에서 0 까지 감소하는 방향으로 잡으면 - 가 되고 변수분리에 의해 양변을 적분하면 t=0 일때 q = q0 이고, t=T/4 일때 q =0 이므로 cosq =2sin2(q/2)-1 이고, sin(q/2)=sin(q0/2)sinφ로 치환하여 식을 정리하면 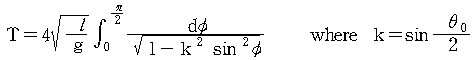 여기서 미소진동 (q0≒0)일때 k=0 이므로 T=2π(ℓ/g)1/2 가 되는 것을 확인할수있고, 위와같은 적분을 타원적분(elliptic integral)이라 부른다. 또, 급수형식으로 주기를 아래와 같이 표현할수 있다. (각자 유도해 보라) Ref 2. 세상에서 가장 빠른 진자 다음 그림과 같이 각각의 진자면에 쇠구슬을 놓고 진동시킬때 어느 것이 가장 빨리 진동할까? (원형곡면 위에서 마찰없이 진동하는 구슬은 실에 매달린 단진자의 경우와 유사한가?) 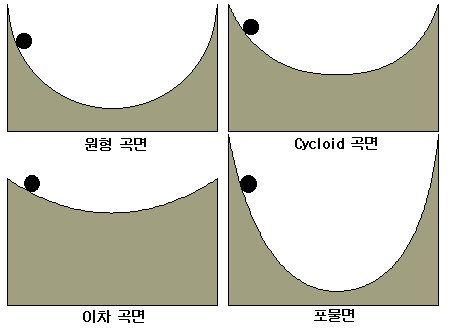
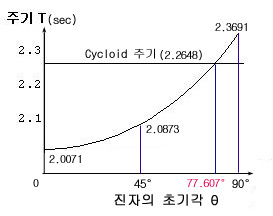
※ 사이클로이드 곡선을 발견하여 명명한 사람은 갈릴레이 이고, 위의 사실은 진자시계의 정확성을 증명하는 과정에서 크리스찬 호이겐스에 의해 발견되었다. 또, 그는 사이클로이드의 축폐선(evolute)은 역시 사이클로이드가 되는 축폐선의 이론을 발견하였다. 그러나, 호이겐스의 이러한 사이클로이드 진자의 등시성 이라는 놀라운 발견에도 불구하고 실제로 진자 시계를 제작할때 호이겐스의 생각은 그리 실용적이지는 못하다. 베셀(Bessel) 등의 연구에 의하면 적당한 추의 길이와 질량을 선택하면 충분한 정도의 등시성이 달성되기 때문이다. 참고로 진자의 길이가 ℓ=1m 일때, 폭이 똑같다는 전제하에 위의 각각의 경우에 대한 주기를 계산해 보는것도 흥미로운 일이다. (1) 원형곡면의 경우는 위의 공식과 같고 (2) Cycloid : x = a(q-sinq), y = -a(1-cosq) 에서 폭이 2 (a=1/π)이면, T=4π√(1/gπ) (3) 포물면의 경우 y=x2 [-1,1] , 진자의 초기위치 높이를 h 로 놓고 계산해 보면 단진자의 주기곡선을 초기각, 0°∼90°구간에서 매스메티카 등의 수학 프로그램 등을 이용하여 그래프를 그려보면 아래 그림과 같다.
[참고 문헌] - SCHAUM'S OUTLINE SERIES "Theoretical Mechanics" 105-107P - Fowles "Analytical Mechanics" 109P |