|
1-1. 자유낙하운동과 포물체 운동
Last Updated 2007/2/29
1. 실험목적
자유낙하하는 물체의 시간에 따른 위치변화를 관찰하고 중력가속도를 측정한다. 또 수평면에 대해 다양한 각도로 물체가 쏘아 올려질 때 물체는 포물선 운동을 함을 이해하고 이 포사체 운동의 실험결과가 이론식과 잘 일치하는가를 알아본다.
2. 원 리
(1)자유낙하운동
자신이외의 다른 아무것에도 영향을 받지 않는 (이를 물리학에서는 고립되었다고 부른다.) 물체는 운동상태를 보존한다. 즉, 정지해 있던 물체는 계속 정지해 있고, 운동하던 물체는 등속도로 운동을 계속한다. 자연의 이러한 특성을 관성의 법칙(law of inertia)이라고 하며, 이러한 물체의 성질을 관성(inertia)이라고 부른다. 물체마다 관성의 정도가 다른데 그 정도를 정량적으로 나타낸 것이 질량(mass), 더 정확하게는 관성질량(inertial mass)이다.
물체의 운동상태를 변화시킬 수도 있는데 그 요인을 힘(force)이라고 하며 운동상태의 변화는 가속도로 나타낸다. 이 힘과 가속도사이의 관계를 뉴턴(Newton)의 제2법칙이라고 부른다.
물체의 운동상태를 기술하는 기본적인 물리량은 속도 v 이다. 물체의 운동상태의 변화는 시간당 속도의 변화량 즉, 가속도 a 로 나타낸다. 물체에 힘이 작용하면 얼마만한 가속도가 생길까? 이 질문은 물체의 운동에 관한 자연의 성질을 묻는 것이기도 하지만 또 다른 한편으로는 자연의 성질(법칙)을 이용하여 우리가 사용할 힘을 정하는 힘의 정의식이기도 하다. 뉴턴이 발견한 운동법칙은 물체에 가해진 힘 F 와 힘에 의한 물체의 가속도 a 사이에 비례관계
F = ma ---------------- (1)
를 갖는 힘을 정의하며, 이때 비례상수 m 이 물체의 (관성)질량이다.
특별히 힘 F 가 일정한 경우에는 식(1)에 따라서 물체의 가속도도 일정하고(물체의 질량 m 이 속도에 무관하게 일정한 경우), 따라서 시간 t 에서의 물체의 속도 v 는
v = vo + at -------------- (2)
이다. 여기서 vo 는 시간 t = 0 에서의 물체의 속도를 가리킨다.
속도와 가속도가 서로 같은 방향(또는 서로 반대 방향)인 경우 물체는 1차원운동을 한다고 말한다. 1차원운동을 하는 물체가 시간 t 동안에 움직인 거리 h 는 식(2)의 적분으로 부터
h = vot + 1/2 at2 ---------- (3)
가 된다.
이제 중력 가속도가 일정한 이유에 대해서 생각해 보기로 한다. 지면위에서 낙하하는 물체에 작용하는 힘은 지구와의 중력(만유인력)이며 중력은 지구(중심)으로부터 물체까지의 거리에 의해서 달라질 수 있을 것이다. 그러나 우리가 실험실에서 취급하는 물체의 크기나 낙하시키는 거리에 비해 지구가 매우 크기 때문에 지구상에서 낙하하는 대부분의 물체의 경우 지구중심 으로부터 물체 까지의 거리는 거의 변하지 않는다고 가정할 수 있다. 따라서 이 실험을 통해서 중력이 거리에 어떻게 의존하는지를 직접 알아내기란 힘들다.
뉴턴의 만유인력 법칙에서는 모든 물체사이에는 서로 잡아당기는 인력이 작용하며 그 크기는 물체간 거리의 제곱에 반비례하고, 두 물체의 (중력)질량에 각각 비례한다고 보았다. 즉, 만유인력의 크기는
F = Gm1m2/r2 --------------- (4)
로 쓸 수 있으며, 여기서 비례상수 G(= 6.67 x 10-11m3/s2kg) 를 만유인력의 상수라고 부른다. 이러한 가정이 성립하는지 여부는 실험에 의해 확인될 수 밖에 없으며, 지금까지의 실험실 규모로부터 천체의 운동 등 광대한 범위에 걸친 수많은 관측을 통하여 식(4)의 표현이 (아직까지는) 정확한 것으로 받아들여지고 있다.
이 실험에서와 같이 지표면으로부터 물체까지의 거리가 지구의 반지름에 비해 매우 작은 경우 물체의 운동에 상관없이 식 (4)에서
r = R (R = 6370 km, 지구의 평균 반지름) ---- (5)
으로 쓸 수 있으므로, 식 (1)과 함께 질량이 M( = 5.98 x 1024 kg)인 지구의 중력에 의해서 자유낙하하는 물체의 중력가속도가
g = GM/R2 = 9.8 m/s2 -------------- (6)
으로 물체에 상관없이 일정함을 알 수 있다. 실제로는 지구의 질량분포가 균일하지 않으며, 구형이 아닐뿐더러 지구의 자전에 따른 영향 등으로 중력가속도는 위치나 시간에 따라서 다소 변화한다. 아래 표는 실제로 위도 45도에서 고도에 따른 g 값의 변화를 표시한다.
[위도 45도에서 고도에 따른 g의 변화]
|
고도(km) |
0.0 |
1 |
4 |
8 |
16 |
100 |
500 |
1,000 |
380,000 |
|
g(m/s2) |
9.806 |
9.803 |
9.794 |
9.782 |
9.757 |
9.60 |
8.53 |
7.41 |
0.00271 | (1,000km : 전형적인 인공위성의 고도, 380,000km : 달의 궤도 반지름)
R = r 로놓고, 식(6)을 미분하면 중심으로부터 거리의 미소변화 dr/r이 중력 가속도의 미소변화 dg/g 와 다음 관계가 있다는 것을 알 수 있다.
dg/g=-2(dr/r)
따라서, 만일 지표면 위로 100m 상승하면 dr/r~ (100m)/(6.4×106m)=1.6×10-5 이고, g는 대략 (-2)(1.6×10-5)≒3×10-5 % 가 변한다. 이것이 지표면 근처에서 g를 상수로 취할 수 있는 이유이다.
우리는 이 실험에서 중력에 의해 물체가 어떻게 낙하하는지 알아보기 위하여 컴퓨터와 포토게이트 센서의 빠른 데이터 처리속도를 이용하여 자유낙하하는 물체(피켓펜스)의 위치(또는 속도)를 시간의 함수로 측정한다. 가속도가 일정하지 않은 경우에는 무엇이 어떻게 달라질 것인지 생각해 보자.
당신의 실험결과는 (중력)가속도가 일정한 경우와 부합하였는가? 그러한 판단의 근거는 무엇인가? 만약 그렇지 못하다면 그 이유에 대해서도 생각해 보라. 이 값은 모든물체, 예컨데 다른 질량, 크기 또는 물성에 대해 모두 같은 값을 가지는가?
(2) 포물체 운동
수직 평면상에서 가속없이 일정한 초기속도로 움직이는 물체는 항상 하단방향의 자유낙하 가속도가 작용한다. 그러한 물체를 포사체(projectile, 발사된 물체라는 의미)라 부르고 이러한 물체의 운동을 포사체 운동(projectile motion)이라고 한다.
어떤 물체가 x축의 양의 방향에 대해 θ 의 각도로 초기속도 v0 로 발사되었다면 (이때 공기의 저항은 무시) x, y 방향의 각각의 속도 성분은
v0x = v0 cosθ , v0y = v0 sinθ
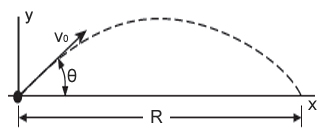
[그림1] 포사체 운동 |
이다. 수평방향의 가속도는 없으므로 양변을 t 에대해 적분하면 (초기조건 t=0 일때 x=0)
x = (v0 cosθ) t -------(7)
수직방향에 대해서는 하단 방향의 중력가속도(g=9.81m/s2)가 작용하므로 vy = v0 sinθ - gt 가되고 마찬가지로 양변을 적분하면 (초기조건, t=0 일때 y=0) |
y = (v0 sinθ)t -1/2 gt2 ----(8)
식 (7), (8)에서 t 를 소거하면
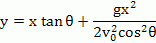 -------------(9)
수평도달거리, R은 y=0 일때 x 값 이므로
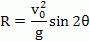 -------(10)
우리는 여기서 발사체의 초기높이는 종단높이와 같다고 가정하였으나 실제실험에서는 발사체가 일정한 높이(y0)에 위치하고 구슬이 스프링에 의해 밀려 발사되기 직전(발사체의 총구에 구슬이 그림으로 표시됨)의 초기 발사높이를 고려해 주어야 겠다.
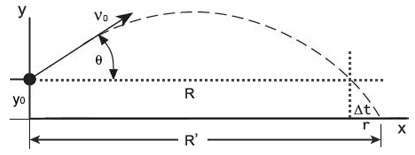 [그림2] 실제 포사체 운동 [그림2] 실제 포사체 운동
총구의 높이를 원점으로 환산하면 실제 수평도달거리, R은 구슬이 나중높이 y0에서 Δt 시간만큼 수평방향으로 더 진행한 거리를 빼 주어야 한다. 식(8)는 초기높이를 고려하면
y = y0 + (v0 sinθ)t -1/2 gt2 -----------(11)
이 되고, 식 (7)과 (11)는 t를 매개로하는 포물선의 방정식이 되겠다. 낙하지점까지 전체 걸린 시간을 tT (y=0 일때 t값), 실제 수평도달거리, R 까지 걸린시간을 th (y=y0 일때 t값)라 하면 Δt = tT - th 이 되므로 계산해보면(각자 유도해 보자)
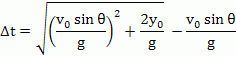 --------(12)
그러므로 실 수평도달거리, R은
R = R'- r = R'- (v0 cosθ) Δt ------------(13)
이 된다. 우리는 이 실험에서 포사체가 포물선 운동을 하는가를 눈으로 확인하고 수평도달거리는 이론식과 잘 일치하는가 알아볼 것이다. 또한 초기발사각이 45° 일때 수평도달거리가 최대가 됨을 실험적으로 확인해보자. 원래 탄환의 속도 측정방법에는 발사체 앞에 포토게이트를 설치하여 측정하거나 수평발사의 경우 수평도달거리를 측정하여 구하는 방법 등이 있다.
여기에 안내된 실험방법은 교과에 맞추기 위해 기본적인 포사체 운동의 내용만을 다루었으나 좀 더 다양한 실험을 위해 어떤 내용들을 고려하고 실험 할 수 있는지 토론해 보자.
3. 기구 및 장치
(1) 컴퓨터 및 인터페이스 장치
(2) 피켓펜스 2종(picket fence; 1cm 또는 2cm 의 검은띠가 아크릴 자)
(3) 포토게이트 및 케이블
(4) A베이스, 지지막대(60cm), 클램프
(5) 바구니(고무패드;충격 완화용)
(6) 고무판(두께3mm, 80x40cm 2장)
(7) 발사체, 범용 테이블클램프, 플라스틱구슬 2개
(8) 포토게이트 브라켓 및 고정나사
(9) 버니어캘리퍼스
(10) 차단막 및 고정클램프(2개)
(11) 먹지 3장, A4용지 4장 이상(조별로 준비  별도로 나눠 주지 않음) 별도로 나눠 주지 않음)
(12) 줄자(2m)
(13) 전자저울(0.01g~300g), 스카치테이프 (공용)
4. 실험방법(권장)
1) 자유낙하운동

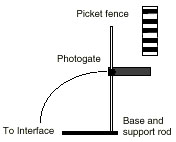
[그림3] 센서의 셋업

[그림4] 중력가속도 측정 셋업 |
(1) 인터페이스 전원을 켠 다음 컴퓨터를 켠다. [주의] 컴퓨터가 외부장치를 인식하도록 컴퓨터를 켜기전 인터페이스 전원을 먼저 켠다.
(2) 데이타스튜디오 프로그램을 실행하고 포토게이트(Photogate & Picket Fence) 아이콘을 디지탈 채널1 로 끌어서 센서를 설치해준다.
(3) 실험장치의 구성은 [그림4]와 같다. A베이스에 지지막대를 세우고 수평조절나사 2개를 잘 조절하여 스탠드의 평형을 잡는다.
(4) 클램프를 이용하여 포토게이트를 수평으로 지지하고 포토게이트의 폰잭을 인터페이스의 디지탈 채널1 에 연결한다.
(5) 실험테이블 위에는 충격흡수용 고무패드가 들어있는 바구니를 올려놓고 피켓펜스가 게이트 사이를 수직으로 떨어지도록 한다.
(6) 먼저 검은띠 2cm인 (투명띠3cm) 피켓펜스로 실험을 수행하기 위해 채널1 아이콘을 더블 클릭하고 Constant 탭에서 band spacing 디폴트 값 0.050(5cm)를 확인하고 그대로 놔둔다. 왜, 이렇게 설정했을까?
☞ 포토게이트 사용법의 시간측정 방식 참조.
(7) 그래프 아이콘  을 채널1로 끌어가서 거리에 대한 그래프윈도우를 띄우고(또는 더블클릭하여 선택), 테이블 윈도우도 띄운다. 을 채널1로 끌어가서 거리에 대한 그래프윈도우를 띄우고(또는 더블클릭하여 선택), 테이블 윈도우도 띄운다. |
[그림5] 피켓펜스의 낙하 |
(8)  버튼을 클릭하여 데이타 저장을 시작하고 자를 떨어뜨린다. 컴퓨터 화면에 시간에 따른 물체의 위치변화 -사실은 포토게이트가 펄스모드에서 검은띠에 의해 가로 막히는 순간의 시간들을 측정-가 측정되어 그래프로 나타난다. 버튼을 클릭하여 데이타 저장을 시작하고 자를 떨어뜨린다. 컴퓨터 화면에 시간에 따른 물체의 위치변화 -사실은 포토게이트가 펄스모드에서 검은띠에 의해 가로 막히는 순간의 시간들을 측정-가 측정되어 그래프로 나타난다.
(9)  ⇒ 오토스케일(Autoscale) ⇒ 오토스케일(Autoscale) 버튼을 클릭하여 그래프의 데이터가 적절한지 여부를 판단하고 그래프가 적절하지 않을 때 좌측상단의 DATA 박스에서 Delete 키를 눌러 데이터를 지운다. 버튼을 클릭하여 그래프의 데이터가 적절한지 여부를 판단하고 그래프가 적절하지 않을 때 좌측상단의 DATA 박스에서 Delete 키를 눌러 데이터를 지운다.
그래프에 나타나는 점들은 피켓펜스의 어느 지점에 해당하는가? 컴퓨터가 속도 그래프를 그려주는 방법은 무엇일까? (게이트모드, 펄스모드, 소숫점계산을 잘 고려해 볼것) |
(10) 5번 이상 측정하여 그래프 데이타를 얻고 실험치를 저장할때는 File-Save Activity As 하여 다른 이름으로 저장한다. 결과보고서에는 초기높이 h0= 0 일 때의 실험데이타 중 잘 나온것 3개를 정리하여 그래프를 붙이고 데이터 테이블에 있는 데이터를 이용, 최소자승법에 의해 측정값들의 분포를 가장 잘 나타내는 직선을 구하고 그 기울기로부터 중력가속도 g 값을 계산해보자.
(11) 피켓펜스를 게이트로 부터 10cm~30cm 위의 높이에서 떨어뜨리면서 위와같은 측정을 반복 해보자. 무엇이 달라졌는가?
(12) 2cm의 검은띠(투명띠 3cm 간격) 피켓펜스에 대해서도 위와같은 측정을 반복하여 데이터를 구하고 이 값으로부터 중력가속도 g값을 직접 계산해보자. 이때 측정 단위가 다르므로 피켓펜스의 띠 간격을 바꿔줘야 할 것이다. 물체의 중력 가속도는 어떠한가? 앞의 경우(질량이 다른 경우)와 어떻게 다른가? 좀더 좋은 2차곡선을 관찰하려면 피켓펜스를 어떻게 바꿀것인가?
*데이터분석 참고
분석하려는 속도-시간의 그래프윈도우에서 Fit => Linear Fit 를 선택하면 직선의 기울기(Slope; 중력 가속도)값이 나타난다. 컴퓨터가 다 계산 해버렸다! 그러나 결과 레포트에는 이 값들을 쓰지말고 참고만 할것. 결과 보고서는 실험을 통해 얻어진 그래프와 데이타 테이블 값들을 사용하여 중력가속도값을 구한다. |
2) 포물체운동
A. 발사체의 발사속도 측정

[그림6] 포토게이트의 설치
(1) 우선 발사체의 장전단계별 발사속도를 측정하기 위해 발사체 총구 앞에 [그림6]과 같이 발사체 앞에 포토게이트를 설치한다.

[그림7] 센서의 셋업 |
(2) 데이터스튜디오 프로그램에서 [그림7]와 같이 포토게이트 아이콘을 선택하고 Measurement 탭에서는 velocity in gate(m/s) 만 선택(디폴트값)하고, Constant 탭에서는 구슬의 직경(0.025m; 버니어캘리퍼스로 측정)을 입력해준다.
(3) Digit 아이콘을 포토게이트 아이콘으로 끌어가서 속도표시창을 띄우고 포토게이트가 구슬이 나오는 정 중앙에 정렬되어 있는지 LED깜빡임을 통해 작동은 잘 되는지 다시한번 확인해 보고 구슬을 1단 장전한다. |
[참고]
포토게이트 2개를 설치하여 2개의 간격를 통과하는 시간을 이용해 속도를 측정할 수도 있겠으나 편의상 1개만 설치한다. 구의 직경거리가 포토게이트의 게이트(감광부, 수광부의 직선부분)를 통과하는 시간을 측정하여 속도를 표시하는 것이므로 초기속도를 정확히 재기 위해서는 게이트를 구슬의 정중앙에 정렬하는 것은 매우 중요하다. |
[주의]
(1) 포토게이트의 정렬상태 확인은 구슬을 그냥 끼워놓은 상태에서 확인(발사되지 않음)하고 장전한 상태에서 눈으로 확인하지 말것. 실수로 발사레버가 건드려 질 경우, 구슬이 발사되어 눈에 부딪히지 않도록 주의!
(2) [그림6] 브라켓에 포토게이트를 고정할 때 긴 나사로 조일 경우, 내부기판이 부서져 고장나므로 주의! |
(4)  시작버튼을 누르고 발사체 레버를 당겨서 구슬을 발사하고 발사체 앞에서 두손으로 쇠구슬을 받아낸다. 속도표시창에 측정되는 속도를 데이터시트에 기록한 다음, 시작버튼을 누르고 발사체 레버를 당겨서 구슬을 발사하고 발사체 앞에서 두손으로 쇠구슬을 받아낸다. 속도표시창에 측정되는 속도를 데이터시트에 기록한 다음,  정지한다. 정지한다.
(5) 구슬을 5회 발사하여 측정되는 속도값을 아래와 같은 데이터시트에 기록하고 2단 장전의 경우에도 위의 과정을 반복하여 속도값을 기록해준다.
발사체의 발사속도 측정 [플라스틱 구슬]
|
시행 |
1 |
2 |
3 |
4 |
5 |
평균속도(m/s) |
|
1단 장전 |
|
|
|
|
|
|
|
2단 장전 |
|
|
|
|
|
| B. 포사체의 운동
[주의]
포사체운동 실험은 플라스틱 구슬로 2단(또는 1단)만 사용하고 모든 실험은 테이블(가로190cm) 위에서만 실시한다.(3단 장전은 사용하지 않음) 고무판 이외의 장소에 구슬이 떨어질 경우, 세게 튀므로 LCD모니터에 부딪혀 파손되거나 구슬을 잃어버리지 않도록 주의한다. |
 [그림8] 포사체운동 셋업 [그림8] 포사체운동 셋업
(1) [그림8]와 같이 테이블의 왼쪽 끝에 발사체를 범용 테이블 클램프를 이용하여 고정하고 테이블의 오른쪽 끝에는 볼이 다른곳으로 튀어가지 않도록 테이블 클램프 2개를 이용하여 차단막을 세운 다음, 우측 끝으로부터 바닥에 고무판(80x40cm) 2장을 깐다.(이 과정은 이미 되어있을 수 있다)
(2) 다음, 조별로 준비된 A4용지 4장을 테이프를 이용하여 길게 연결하고 [그림8]과 같이 A4용지는 고무판에 테이프를 이용하여 고정 (움직이지 않을 정도로만)한 다음, 그 위에 먹지(3장 연결된 것)를 올려놓는다. (이때 먹지는 수시로 들어내어 확인해야 하므로 테이프로 고정하지 않음! 테이프로 먹지를 고정할 경우 먹지가 찢어짐)

[그림9] 발사체의 각도조정 |
(3) 발사체에 나무막대를 이용하여 플라스틱 구슬을 2단 장전하고 발사체의 각도계를 20°로 조정한다. 구슬의 초기높이 y0 를 측정하여 기록해 둔다.
[참고]
발사체의 각도조정은 [그림9]과같이 총구부분의 측면나사는 고정하고 뒷부분의 나사를 움직여가며 각도를 조정해준다. 구슬이 내부에서 피스톤에의해 발사되는 순간,구슬의 초기위치의 중심은 상단 고정나사와 일치하도록 제작되어있다. |
(4) 발사레버를 당겨서 구슬을 발사하고 먹지위에 떨어짐을 확인하고 먹지를 들어내어 찍혀진 착지점의 중심을 20°#1 등으로 표시한다. 불필요한 착지점이 찍혀있을 경우, 나중에 혼란을 방지하기위해 미리 x표시를 해두고 다시 먹지를 종이위에 덮는다. 같은 각에 대해 5회 실험을 반복하여 착지 지점을 표시하고 수평도달거리 R' 를 자로 측정하여 기록한다. (단위는 모두 cm, 소수 첫째자리로 통일하여 기록)
(5) 발사각을 30°, 45°, 60°,70° 로 바꿔가며 위의 과정을 반복하여 실험하되 각도를 변화시키는 동안 구슬의 초기높이 y0 가 변하지 않도록 조심스럽게 조정해 나간다.
|
(6) 실제 수평도달거리를 계산하고 이론값과의 오차를 계산해본다. 1단 장전의 경우에도 위 실험을 반복해보고 실험데이터를 정리해보자. 오차가 크다면 어떤방법으로 실험해야 좀 더 계산된 실험을 수행할 수 있을까 토의해 보자.
발사각의 변화에 따른 수평도달거리 측정 [플라스틱 구슬]
| 경사각 |
20° |
30° |
45° |
60° |
70° |
| 1회 |
|
|
|
|
|
| 2회 |
|
|
|
|
|
| 3회 |
|
|
|
|
|
| 4회 |
|
|
|
|
|
| 5회 |
|
|
|
|
|
| R'(평균;cm) |
|
|
|
|
|
| |
20° |
30° |
45° |
60° |
70° |
| Δt (sec) |
|
|
|
|
|
| r=Δt v0 cosθ (cm) |
|
|
|
|
|
| Rm = R'-r (cm) |
|
|
|
|
|
| R(이론치;cm) |
|
|
|
|
|
| 오차(%) |
|
|
|
|
|
[실험후 정돈 주의사항]
잦은 해체와 조립으로 인한 파손을 방지하지 위해 발사체는 [그림8]과 같이 그대로 테이블에 고정해 놓고 먹지는 찢어지지 않도록 사용 후, 비닐에 넣어 보관하고 나머지 부품은 조별로 섞이지 않도록 박스에 담아 놓는다. |
5. 참 고 (Reference)
(1) Acceleration of a Freely Falling Picket Fence (PDF 파일)
(2) 버니어캘리퍼스 / 포토게이트 / 전자저울
|
 실험실소개
실험실소개
 실험실위치
실험실위치
 오시는길
오시는길