연세대학교 물리학실험실(Yonsei Phylab)

1-5. 관성모멘트와 각운동량 보존

(Last Updated 2007/3/13)

1. 실험목적

회전 역학계에서 여러모양의 물체, 원반, 링, 막대 등의 회전에 의한 관성모멘트를 측정하여 관성모멘트 개념을 이해하고 각운동량의 보존 여부를 조사한다.

2. 이 론

(1) 관성모멘트

미식축구에서 쿼터백은 공을 더 멀리 던지기위해 타원형의 공이 장축을 중심으로 나선형으로 날아가도록 볼을 던진다. 빙판위의 피겨 스케이팅 선수는 회전속도를 증가시키기위해 바깥쪽으로 뻗어진 두팔을 몸 가까이로 오므린다. 이러한 두가지 현상에 있어서 관성모멘트는 중요한 역할을 한다.

물체의 관성모멘트는 질량과 질량의 공간적 분포에 의존한다. 일반적으로 물체가 더욱 밀집 될수록 관성모멘트는 작아진다.

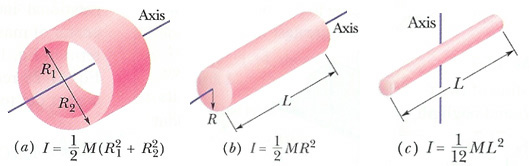
[그림1] 물체의 관성모멘트
회전운동에서 여러 가지 물체에 대한 이론적인 관성모멘트 값은 [그림1]과 같다. (각자 유도해 보자) 물체의 관성모멘트를 측정하려면 어떻게 해야할지 생각해보자.

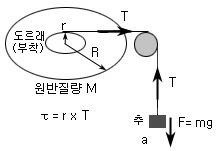
[그림2] 관성모멘트 측정장치 고안

원반의 회전운동에서 실험적인 값을 구하기 위해 [그림2]와 같이 장치를 고안해보자. 작용하는 토오크와 각 가속도가 측정되면 τ = Iα로 부터

I = τ/α ---------------(1)

여기서 α는 각 가속도이고 τ는 토오크이다. 원반의 중심으로부터 거리 r 되는 지점에 힘 F 가 가해질 때 토오크는τ = r×F 이고
이 경우 작용한 힘은 도르래에 의해 연결된 줄에 작용하는 장력 T 와 같다.

줄은 매달린 질량 m 에 의해 당겨지고 r은 회전하는 원반의 중심에 고정 부착된 도르래(질량무시)의 반지름 이다.
반지름 r 은 작용하는 힘(장력) T 에 대해 수직이므로

τ = rT ---------------(2)

이고, 매달린 질량 m 에 대한 뉴튼의 제2법칙은

∑F = ma = mg-T---------------(3)

이므로 T= m(g-a) 이다. 이 식을 (2)에 대입하면

τ = rT = rm(g-a) ----------------(4)

매달린 질량의 직선가속도 a 는 회전계의 접선가속도 a_T 와 같고 각 가속도는 접선가속도와 다음과 같은 관계가 있다.

α = a_T/r -----------------(5)

식 (4),(5)를 (1)에 대입하면

I = τ/α= rm(g-a) / (a_T/r) = mr²(g/a-1) ----(6)

위와같이 물체의 관성모멘트 I 는 도르래를 통해 매달린 질량 m에 의해 회전계가 회전할때 접선가속도 a를 측정 하므로써 구할수 있다.
또는 위의식 식(6)을 질량 m인 추가 정지상태에서 t초 동안 h 거리 만큼 떨어지면서 원판을 회전시킬 때 에너지 보존법칙의 관점에서도 유도해보자.

(2) 각운동량 보존

자유롭게 회전하는 물체에 토오크 τ가 가해질때, 물체의 각운동량은 변화한다.
원반 디스크가 회전하고 있는 계에서 다른 물체를 올려 놓으면 계의 회전속도가 달라진다. 물론 계에 작용하는 외부 토오크는 없다.
여기서 I_d 는 디스크의 관성모멘트, I_o 는 다른물체의 관성모멘트라고 하면 계의 총 각운동량은 보존되므로

L= I_i ω_i = I_f ω_f----------(7)

여기서, I_i = I_d , I_f = I_d + I_o 이므로 원판의 최종 각속도는

ω_f = (I_i/I_f)ω_i = [I_d/(I_d+I_o)] ω_i-----(8)
이 되고 I_d = I_o 일 경우, ω_f = ω_i/2 이 될 것이다.

우리는 이 실험에서 원판게이트 와 포토게이트를 이용하여 자유롭게 회전하는 물체의 회전각속도를 측정하고 PC 인터페이스를 이용하여 각속도의 변화를 관찰할 것이다.

3. 실험기구 및 장치

(1) 컴퓨터 및 인터페이스 장치
(2) 관성 모멘트 측정장치 세트
   ① 원반 2개 (885g, R=10cm, 중앙홈 r=0.238cm)
   ② 링 (368g, 내경 R₁=5cm, 외경 R₂=6cm)
   ③ 추걸이(5g), 추(20g×3개, 10g, 5g), 수평계
   ④ 원판게이트, 3단도르래(반경=2.8, 2.05, 1.3cm)
   ⑤ 도르래지지대, 중심축
(3) 포토게이트/도르래(스마트풀리, r=2.54cm)
(4) A 베이스
(5) 버니어 캘리퍼스
(6) 실, 추2g (8개), 투명테이프(공용)
(7) 전자저울(0.01g~2kg,공용)

4. 실험방법

(1) 컴퓨터 셋업

[그림3] 센서의 셋업

① 인터페이스 전원을 켠 다음 컴퓨터를 켜고 데이터스튜디오 프로그램을 실행한다.

② 스마트풀리 잭을 디지털 채널1에 연결하고 프로그램에서도 [그림3]과 같이 채널1 에 Smart Pulley 를 설치한다. 스마트풀리 아이콘을 더블클릭-Measurement 탭에서는 Velocity Ch1(m/s)만 선택, Constant 탭은 디폴트값(Spoke Arc length; 0.015m)을 그대로 쓴다. 이 값은 무엇을 의미하는가?

③ 다음 그래프 아이콘

을 스마트풀리 아이콘으로 끌어가서 속도-시간의 그래프를 띄운다.

(2) 관성모멘트 측정

1) 축 자체의 관성모멘트 측정

① 먼저 3단도르래의 직경 3개를 버니어캘리퍼스로 측정하여 반지름 값을 기록해 놓고 실을 약120cm 정도 잘라낸다. [그림4]와 같이(원반만 제외) A베이스에 중심축을 세우고 3단도르래를 씌운 다음 스마트풀리를 설치한다.

② 3단도르래 구멍에 실을 끼워 하단의 나사부분에 2~3번 감고(묶지 않고 편리하게 다시 풀어쓸수있다) 실의 한쪽 끝은 질량 2g (또는 5g 추걸이)을 매달아 스마트풀리에 걸어놓는다.(추에 실을 묶기가 어려우면 작은 투명테이프로 붙인다)

③ 장치의 측면과 상단에서 보았을때 실이 풀리에 일직선으로 걸리도록 수평을 잘 맞추고 추가 거의 스마트풀리까지 올라오도록 3단도르래에 실을 감고 정지상태를 유지한다.

④ 회전체를 놓으며

버튼을 눌러 데이타 저장을 시작하고 추가 거의 바닥에 내려오기 전 재빨리

버튼을 누른다. (추의 낙하속도가 너무 빠르거나 느리면 오차가 많이 발생할 수 있으므로 추의 질량이나 3단도르래의 반경을 잘 선택해야 한다.)

⑤ 속도-시간의 그래프로부터 Curve Fit ⇒ Linear Fit 로부터 그래프의 최적곡선의 기울기(가속도)를 구하고 식(6)으로부터 자체 관성모멘트 I 를 계산한다.

⑥ 위의 과정을 5번 되풀이하고 평균하여 축자체의 관성모멘트 값(g cm² 으로 표시)을 구하고 데이터를 기록해 놓는다.

2) 원반(Disk)

[그림4] 원반의 관성모멘트 측정

① 측정할 원반의 반지름과 질량을 재어 데이터를 기록하고 원반을 밑의 홈에 잘 맞추어 회전축 위에 올려놓는다.

② 원반위에 수평계를 올려놓고 원반이 수평이 되도록 A베이스의 수평조절나사를 이용하여 잘 맞춘다.

③ 실끝에 약 50g 질량을 매달고 추가 거의 스마트풀리까지 올라오도록 3단도르래에 실을 감고 정지상태를 유지한다.

④ 회전체를 놓으며

버튼을 눌러 데이타 저장을 시작하고 추가 바닥에 거의 내려왔을 때

버튼을 누른다.

⑤ 그래프로부터 위의 방법과 같이 접선가속도를 구하고 회전계의 관성모멘트를 계산한 다음, 축에 의한 값을 빼주면 원반의 관성모멘트값이 될 것이다.

⑥ 위의 과정을 5번 반복하여 실험하고 이론치와 비교하여 % 오차를 계산한다. 원반에 대한 관성모멘트(이론치)는 실제모양과 비교해 볼때 정확한 값인가? 실제 모양에 의한 모멘트값은 이론치 보다 크겠는가? 작겠는가? 토의해 보자.

⑦ [그림5]와 같이 원반을 수직으로 세우고(측면 나사탭이 뚫려있는 원반을 오른나사 방향으로 조여준다) 위의 과정을 반복하여 원반이 수직으로 회전할 때의 관성모멘트값을 구한다. 수직원반에 대한 관성모멘트 공식을 유도해보고 측정치와의 오차를 계산해보자.

[그림5] 수직원반의 관성모멘트

[그림6] 링의 관성모멘트

3) 링(Ring)

① 링의 내경, 외경과 질량을 재어 데이터를 기록하고 [그림6]과 같이 원반위에 링을 올려놓는다.

② 추의 낙하속도가 너무 빠르거나 느리지 않도록 추를 선택하고(약 80g) 위의 과정을 반복하여 전체 관성모멘트 값을 측정한다. 링의 관성모멘트는 전체 값에서 원반 및 축의 관성모멘트 값을 빼주면 될 것이다. 5번 반복하여 실험하고 링에 대한 관성모멘트 이론값과의 오차를 계산한다.

③ 실험데이터 구분을 잘 하여 저장해준다. 위의 방법말고 관성모멘트를 측정하는 방법에는 어떤 것이 있을까?

(3) 각운동량 보존

[그림7] 각운동량의 변화 측정

① 실험장치로부터 3단도르래와 추를 제거하고 [그림7]과 같이 중심축에 원판게이트를 씌운 다음, 스마트풀리에서 도르래를 제거하고 포토게이트를 측면에 설치한다.

② 원판게이트 상단의 홈에 잘 맞추어 다시 원반을 올리고 원반이 회전할때 포토게이트가 원판게이트에 의해 잘 동작하는가를 확인한다. (붉은색 LED가 점멸됨)

③ 프로그램 상단에서 File ⇒ New Activity 하여 장치를 초기화하고 다시 셋업한다.

④ 우리는 여기서 원판게이트를 이용하여 원반의 회전 각속도만을 측정하므로 디지털채널1에 스마트풀리(Smart Pulley) 를 설치한 다음, 아이콘을 더블클릭, Measurement 탭에서 Angular Velocity Ch1(deg/s)만 선택한다.

[참고] 원판게이트에는 10개의 홈이 일정한 간격으로 만들어져 있으므로 Constant 탭의 바퀴살의 각간격(Spoke Angle Spacing)은 36° 값을 갖는다. 만약 홈이 20개라면 이 값은 얼마로 고쳐주어야 할까?

⑤ 수평계를 이용하여 원반의 수평상태를 다시한번 잘 맞추고

그래프 아이콘을 스마트풀리로 끌어가서 각속도의 그래프를 띄운다.

⑥ 원반을 회전시키고 데이터 저장

을 시작하면 그래프 상에 회전각속도가 표시될 것이다.

⑦ 질량이 같은 다른 원반을 중앙홈을 맞추어 떨어뜨리고 -회전하는 원반에 최대한 충격이 가해지지 않도록 1cm 정도의 높이에서 정확하게 중앙 홈위에 내려 놓는다- 각 속도의 그래프를 관찰해보자. 각속도에는 어떤 변화가 일어나는가?

를 이용하여 초기 각속도와 나중각속도를 각각 측정하고 이론치와 실제 각속도 사이의 오차(%)를 계산해 본다.

⑧ 원반 뿐만아니라 링을 내려놓을 때도 각속도의 변화를 관찰해보자. 이러한 실험들로부터 각운동량은 보존된다고 말할수 있는가?

[주의] 원반이나 링(재질: 알루미늄)을 바닥에 떨어뜨리면 모양이 쉽게 변형되므로 떨어지지 않도록 주의한다.

[질문] 만약 두 개의 원반(또는 링)이 같이 회전하고있는 상태에서 상단 원반(또는 링)을 재빨리 들어낸다면 어떻게 될까? 이 경우도 각운동량은 보존 된다고 말할수 있는가? 원반을 내려놓는 경우와 어떤 차이가 있는가?

5. 참 고

(1) Rotational Inertia / Conservation of Angular Momentum (PDF 파일)

(2) 스마트풀리

(3) 관성모멘트와 각운동량 보존 예