연세대학교 물리학실험실(Yonsei Phylab)

1-9. 파동(줄의진동, 관의공명)

Last Updated 2011/2/24

1. 실험목적

진동하는 줄(횡파) 내에서 정상파를 관찰하고 줄의 장력, 길이, 진동주파수, 정상파 내의 마디수 등의 이론적 관계식이 실험과 일치하는가를 확인한다. 또 관 내부에서 일정한 주파수의 음파(종파)가 전파될때 관의 길이의 변화에 따른 음파의 공명현상을 이해하고 그때의 정상파 모양을 관찰하여 공기중의 음속을 측정한다.

2. 원 리

A. 줄의 진동

양쪽 끝이 고정된 줄(String)을 진동시키면 줄을 따라 진동수와 진폭이 같은 두 파동이 양 끝에서 반사되어 서로 반대방향으로 진행하게 된다. 이러한 파동은 일반적인 간섭법칙에 따라 결합하는데 어떤 조건(공명) 하에서는 정상진동의 형태인 정상파(Standing Wave)가 생긴다. 즉, 기본주파수 또는 그 정수배로 줄을 진동시키면 줄 내에서 정상파가 형성되고 이때 높은 주파수를 배음(harmonics)이라 부른다.

[그림1]과 같이 질량 선밀도 μ인 줄에 장력 T 가 작용하고 있을때 속도 v로 진행하는 정상(stationary)펄스가 있다고 가정하면, 펄스의 미소부분에 대해 수평성분의 힘은 0 이되고 수직성분의 힘은 복원력 F 로 나타날것이다.

F = 2Tsinθ≒ T(2θ) = T(Δℓ/R)

Δm = μΔℓ, a = v²/R

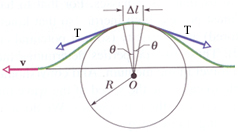
[그림1] 파동의 전파모양

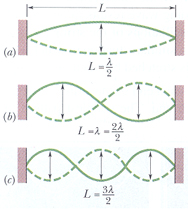
[그림2] 줄의 진동모드

이므로 뉴튼의 제2법칙 F= ma 에 의해

T(Δℓ/R) = (μΔℓ)v²/R

이되고, 따라서 줄에 전달되는 횡파의 속도 v는

v = (T/μ)^1/2--------(1)

이다. [그림2]와 같이 줄의 길이가 고정되어 있다면 정상파의 파장 λ는

λ= 2L/n (n=1,2,3 ) ------(2)

이므로 f = v/λ 관계식으로부터 고유진동수 f 는

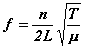---------(3)

으로 표시되고, 식을 변형하면 질량 선밀도 μ는

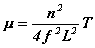-----(4)

이다. 여기서 n은 정상파의 배의 수와 같으며 n=1 일때가 기본진동이고 n=2,3,... 일때가 2배, 3배,...진동이 된다. 만약 장력과 길이가 일정할때 주파수를 변화시키면 주파수와 배의 수는 비례 할것이다.

B. 음파(관의공명)

스피커의 진동판이 진동하면 음파가 공기중으로 전파된다. 음파는 스피커의 진동판 쪽으로 가까워지고 멀어지고 하는 공기분자의 작은 운동으로 이루어져 있다. 만약 스피커 근처의 작은 공기 체적을 볼수 있다면 그 공기 체적이 스피커로부터 멀리 이동하는것이 아니고, 스피커 떨림의 진동수로 스피커로부터 가까워지고 멀어지고 하는것을 볼 수 있을 것이다. 이 운동은 줄(string)의 파동전파와 매우 유사하다. 중요한 차이점은 줄(String)에서의 진동 운동은 파동의 전파 방향에 수직(횡파)이지만, 음파는 전파방향과 같은 방향이다. 그래서 음파를 종파(longitudinal wave) 라고 한다. 또한 음파는 매질 속에서 밀함(compression)과 소함(rarefaction)을 반복하면서 진행한다. 스피커의 진동판이 앞쪽으로 움직이면 진동판 근처의 공기는 비교적 높은 공기 압력의 작은 체적이 만들어져 밀하게 된다. 이 작은 고압력의 공기 체적은 근처의 공기를 밀하게 하고 스피커로부터 멀리 전파되게 한다. 반대로 스피커의 진동판이 안쪽으로 움직이면 진동판 근처의 공기는 비교적 낮은 공기 압력의 작은 체적이 만들어져 소하게 된다. 이 소 역시 스피커로부터 멀리 전파된다.
일반적으로 소리는 모든 방향으로 전파 되지만 우리는 이 실험에서 직선형 관을 이용하여 일차원의 전파로 단순화하기로 한다.

(1) 관 내에서의 정상파(Standing Wave)

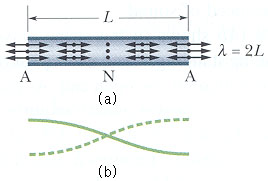
[그림3] 관내에서 기본 정상파

(a) 관내에서 마디(N)는 중앙에 배(A)는 양쪽 끝에 있다. (b) 대응하는 줄의 정상파

정상파는 파동이 줄의 한쪽 끝에서 반사되어 되돌아오는 파동과 원래 진행하던 파동사이의 간섭에 의해 만들어 진다. 또한 음파가 관의 한쪽 끝에서 반사되어 질때도 정상파가 만들어 진다. 줄에서 정상파는 배(antinode)와 마디(node)를 가지고 있다. 배는 정상파에서 진폭이 최대 진폭을 가지고 위 아래로 진동하고, 마디에서는 줄이 움직이지 않는다. 이와 유사하게 음파에서의 정상파도 변위 배(공기 진동의 진폭이 최대)와 변위 마디(공기가 진동하지 않음)를 가지고 있다.

압력마디와 배도 파형안에 역시 존재한다. 사실 압력마디는 변위배에서 일어나고 압력배는 변위마디에서 일어난다. 이것은 압력배가 서로 180 °위상차로 진동하는 두 변위배 사이에 놓여 있다고 생각함으로서 이해할수 있다.

두 변위배의 공기가 서로 마주보고 움직일때 압력배의 압력은 최대이고 멀어져 갈때의 압력은 최소이다.
음파의 반사는 관의 끝이 열려있거나 또는 막혀있는 경우 모두에서 일어난다. 만약 관의 끝이 막혀 있으면 공기는 더 이상 갈데가 없고 따라서 변위마디가 관의 끝에 있게된다. 만약 관의 끝이 열려있으면 압력은 거의 대기압으로 변위배는 열려진 관의 끝에 있게된다.

(2) 공 명 (Resonance)

관속에서 음파는 양쪽 끝사이를 오가면서 여러번 반사되고, 반사되는 동안 서로 중첩되어 일반적으로는 작은 진폭을 보일 것이다. 하지만 모든 반사파가 같은 위상을 가지고 있을때 최대 진폭을 갖게 된다. 이때의 주파수를 공명 주파수라고 한다. 공기중에서 이론적인 음파의 속도는 다음과 같다.

음속 v = 331.5×(1+T/273)^½≒ 331.5 m/s + 0.607 T (T:섭씨온도)

막힌관과 열린관에서 공명 조건을 살펴보면

막힌관 : L = nλ/ 4 (n=1,3,5,7…)
열린관 : L = nλ/ 2 (n=1,2,3,4…)

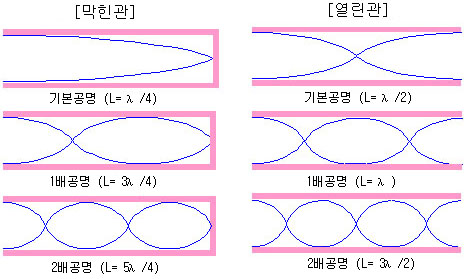
[그림4] 관내의 정상음파
하지만 실험적으로는 관의 끝에 정확히 마디나 배가 만들어 지지않는다. 그것은 관의 끝부분에서 음파의 행동이 주파수와 관의 직경과 관계가 있기 때문이다. 그렇기 때문에 끝 보정을 해주어야 한다. 끝 보정인자는 보통 0.2~0.8정도이며, 여기서는 막힌 관에서는 0.6, 열린 관에서는 1.2 로 하였다. (d:관의 직경)

막힌관 : L + 0.6d = nλ/ 4 (n=1,3,5,7…) --------------(1)
열린관 : L + 1.2d = nλ/ 2 (n=1,2,3,4…) --------------(2)

우리는 이 실험에서 일정한 주파수 음을 내주는 스피커와 음압을 전위차로 바꿔주는 마이크, 그리고 그 전압을 고속으로 샘플링(초당 2만개의 전압값)하여 모니터링 해주는 컴퓨터 인터페이스를 이용해서 막힌관에서 관의 길이를 (피스톤으로) 변화시킬때 공명을 일으키는 위치들을 찾고 측정된 관의 길이로 부터 파장을 구하여 관계식, v = f λ로 부터 음속을 계산할 것이다.

[참고] 매질에 따른 음파의 속도

물질의 상태	종류	속력(m/s)
기체	공기(0℃,1기압)	331
	공기(20℃,1기압)	343
	헬륨	965
	수소	1284
액체	물(0℃)	1402
	물(20℃)	1482
	바닷물(20℃3.5%염도)	1522
고체	알루미늄	6420
	철	5941
	화강암	6000

3. 실험 기구

(1) 컴퓨터, 모니터 및 인터페이스 장치
(2) 파워앰프(Power Amplifier)
(3) 줄(string; 가는줄, 굵은줄 2종)
(4) 파형 구동자(Wave Driver)
(5) 테이블 클램프 2개
(6) 지지막대(30cm), 도르래
(7) 추걸이(50g), 질량세트(500g,100g×4개,50g)

(8) 줄자, 검은 종이판 1장(optional)
(9) 관의 공명장치 (투명한 플라스틱 튜브, 길이 90cm, 내부직경 d= 38mm)
(10) 핀 마이크 (1.5V 밧데리 내장)
(11) 전압센서(Voltage Sensor)
(12) 쇠막대 (마이크용 탐침막대 50cm)
(13) 리드선(2m) 2개

4. 실험 방법

A. 줄의 진동

(1) 가는줄의 진동

실험에 앞서 먼저 우리는 줄에 대한 선밀도를 결정(선밀도가 일정하다고 가정)한 다음 두가지 방법으로 실험을 진행한다.
-첫 번째, 주파수를 변화(길이 일정)시킬때 주파수(f) 대 배의 수(n) 의 그래프의 기울기로 부터 줄의 선밀도를 계산.
-두 번째, 길이를 변화(주파수고정)시킬때 길이(L) 대 배의 수(n) 의 그래프의 기울기로 부터 줄의 선밀도를 계산.
그리고 각각의 경우에대해 직접 측정하여 얻은 선밀도 값에 대한 오차를 계산할 것이다.

가는줄 선밀도: μ= 3.02×10^-4 (kg/m)

☞ 이 값은 일정한 줄의 길이(7.68m ; 240cmx32개)의 질량을 측정(23.16g)하여 구한 값이다.

[그림5] 인터페이스 연결

(1) 인터페이스 전원을 켠 다음 컴퓨터를 켜고 데이터스튜디오 프로그램을 실행한다.

(2) 파워앰프의 딘(DIN) 플러그를 채널A 에 연결하고 프로그램에서도 파워앰프를 설정한다.

a. 주파수변화(길이와 장력 고정)에 따른 줄의진동

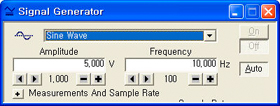
[그림6] 신호발생기의 설정

(3) [그림6]와 같이 신호 발생기에서 파형은 사인파(Sine Wave), 전압진폭은 5V, 주파수는 10Hz, Auto로 놓은 다음, 파워앰프 전원을 켠다.

(4) 장비를 [그림7]과 같이 설치한다. 테이블의 양끝에 테이블클램프를 설치하고 왼쪽에는 지지대, 오른쪽에는 도르래를 설치한다.

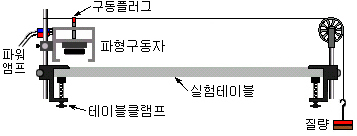
[그림7] 줄의 진동 실험장치(주파수변화)

(5) 파형구동자의 홀더를 왼쪽의 지지대에 걸어 고정하고 줄을 지지대에 걸고 구동플러그의 홈에 끼운다.

(6) 오른쪽에는 줄에 추걸이(50g)를 걸어놓고 줄이 수평이 되도록 왼쪽 고정점과 도르래의 위치를 잘 조절한다. ☞자를 사용하여 줄의 왼쪽, 오른쪽 높이가 같은가를 확인해보자.

(7) 파워앰프의 출력단자를 파형구동자의 입력단자에 연결하고 전원(뒷면스위치)을 켠다.

(8) 질량 1kg 을 매달고 줄자로 줄의 길이(L)를 측정하고 기록한다. 줄의 길이 L은 어디서부터 어디까지 재야할까?

(9)

를 클릭하여 주어진 주파수에 대한 줄의 진동양상을 관찰한다. 우리는 줄의 선밀도를 모르고 순전히 실험적으로 선밀도를 측정한다는 자세로 실험을 진행해야 한다.

(10) 줄이 어떤 주파수에서 기본모드(중앙에 1개의 배만 형성)로 진동하는가를 알아보기 위해 주파수를 1Hz씩 증가시키면서 진동을 관찰한다. 진폭이 근방의 주파수에 비해 대략 최대가 되는 지점에서 0.1Hz 씩 변화시켜가며 더욱 주의깊게 관찰하여 기본진동이 될때의 주파수를 결정한다. ☞ 진동을 더 잘보기 위해 검은 종이판을 이용.

(11) 장력과 길이가 일정한 상태를 유지하며 다시 주파수를 변화시켜 갈때 배진동 즉, n=2, 3... 5 이 형성되는 주파수를 찾아내고 데이터를 기록한다.

(12) n : f 의 직선 그래프를 그리고 이 직선의 기울기를 구한 다음, 줄의 선밀도를 계산한다. 또 직접 측정한 선밀도 값에대한 오차(%)를 계산한다.

(13) 질량을 500g 으로 바꾸고 위의 과정을 반복하여 실험해 보고 데이터를 기록한다.

b. 길이변화(주파수와 장력 고정)에 따른 줄의진동

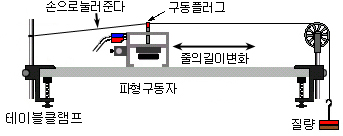
[그림8] 줄의 진동 실험장치(길이변화)

(1) 고정되어 있던 파형구동자를 빼고 [그림8]과 같이 실험장치를 바꾸고 줄의 수평을 잘 맞춘다.

(2) 신호발생기에서 주파수를 150Hz 로, 질량은 500g 으로 고정한다.

(3)

를 누르고 진동하는 파형구동자를 잘잡고 줄을따라 직선상에서 천천히 움직이며 줄의 진동양상을 관찰한다.

[주의] 이때 정상파가 지지대측 줄의 진동에 의해 다시 영향을 받지 않도록 [그림6]과 같이 줄을 손으로 눌러준다.

(4) 줄이 어떤길이에 대해 진폭이 최대가 되는가를 유심히 관찰하고 기본진동을 일으킬 때의 줄의 길이를 자로 측정하여 기록한다.

(5) 진폭 차이가 미소할 때 검은 종이판을 배경으로 사용하여 주의깊게 관찰하고 n=2, 3, 4 일 때, 줄의 길이를 차례로 측정하여 데이터를 기록한다.

(6) n : L 의 직선 그래프를 그리고 이 직선의 기울기를 구한 다음, 줄의 선밀도를 계산한다. 또 직접 측정한 선밀도 값에대한 오차(%)를 계산한다.

(2) 굵은 줄의 진동

굵은줄의 선밀도 값
(1) 500g일때: 선밀도 μ= 9.49×10^-3 (kg/m)
(2) 1000g일때: 선밀도 μ= 7.79×10^-3 (kg/m)

다음, 굵은줄에 대하여 주파수를 변화시켜가며 위의 실험과정을 수행해보자. (여기서 줄의 길이 변화 실험은 하지 않는다)

(1) 줄의 장력은 500g (또는 1000g)으로 잡고 주파수는 1Hz로부터 (사인파(Sine Wave), 전압진폭은 5V) 1Hz씩 증가 시키며 파형을 관찰하고 위의 실험과정을 반복한다.

(2) 가는줄과 굵은줄은 어떤차이가 있는가? 시각적으로 관찰이 용이한 굵은줄에 대하여 선밀도에대한 실험값과 이론값은 일치하는가? 각각의 줄에대하여 토론해보자.

B. 음파(관의 공명)

[그림9] 인터페이스 연결

(1) 인터페이스 전원을 켠 다음 컴퓨터를 켜고 데이터스튜디오 프로그램을 실행한다.

(2) 전압센서를 아나로그 채널A 에, 파워앰프의 딘(DIN)컨넥터를 채널B 에 연결하고 프로그램에서도 [그림9]와 같이 채널A-전압센서(Voltage Sensor)를, 채널B- 파워앰프를 설정해준다.

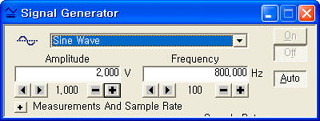
[그림10] 신호발생기의 설정

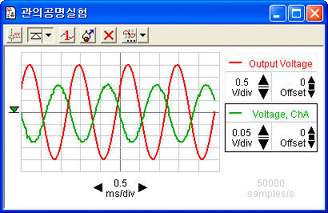
[그림11] 스코프의 설정

(3) 신호발생기는 [그림10]과 같이 사인파(Sine Wave), 전압진폭은 2V, 주파수는 800Hz, Auto로 놓은 다음, 파워앰프 뒷면의 전원을 켠다.

(Auto로 놓으면 실험을 시작할때 신호발생기가 자동으로 동작하여 스피커가 진동한다.)

[주의] 마이크가 고장나므로 전압진폭을 3V 이상 올리지 말 것.

(4) 좌하단 스코프 아이콘을 좌상단 출력전압(Output Voltage)으로 끌어가서 스코프윈도우를 만들고 다시 생성된 좌하단 Scope1 아이콘을 Voltage, ChA로 끌어가면 [그림11]와 같이 된다.

[참고]

스피커를 진동시키기위한 입력신호(적색)와 마이크를 통한 출력신호(음압; 녹색) 2가지를 동시에 보기위해 [그림5]와 같이 스코프를 구성한 것이며 실험중 출력상태에 따라 ms/div와 스케일을 적당히 조절하며 관찰한다.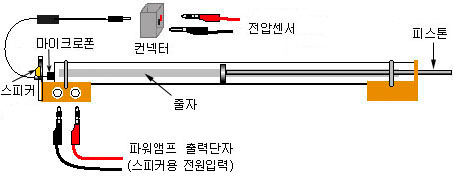

[그림12] 관의 공명장치 셋업
(5) [그림12]와 같이 장치를 설치한다. 파워앰프 출력단자(전압출력)는 관 하단부분의 잭에 연결(스피커 진동용)하고 마이크로 폰은 컨넥터를 통해 전압센서에 연결한다.

[주의]

음압측정용 마이크 연결 커넥터에 파워앰프 출력(전원입력)을 할경우, 마이크가 고장나므로 실험전에는 반드시 배선상태를 확인받는다.

(6) [그림12]의 좌측과 같이 스피커 측의 관을 조금 열어놓고(왜 이렇게 했을까?) 마이크가 관끝에 위치하도록 하고 마이크의 스위치를 켠다.

(7) 시작버튼

을 누르고 피스톤을 완전히 넣은 상태에서 바깥쪽으로 서서히 당기면서 스코프의 파형을 관찰하고 진동음의 크기를 주의깊게 듣는다. 파형이 잘 나타나지 않을때는 [그림5]의 하단과 우측에있는 화살표를 적당히 조절(ms/div와 V/div 스케일 조정)하여 관찰한다.. (실제로 [그림5]와 같은 파형이 나타날것이다. 녹색은 입력파형을 적색은 마이크로폰을 통한 출력파형을 나타낸다.)

(8) 소리와 출력 파형이 극대(증가하다가 감소하기 시작 할 때)가 되는 지점에서 피스톤을 고정하고 관의 길이를 내부에 부착된 자를 통해 읽고 기록하라. 이때가 소리 주파수 800Hz에 대해 공명이 일어나는 관의 길이이다. 피스톤을 뺄 때(관의 길이증가) 공명이 일어나는 위치를 찾으며 기록하고 그에 해당하는 기본공명과 배수공명을 구분하여 n=1, 3, 5... 일 때 관의길이를 적는다.

(9) 실험이 끝나면 정지버튼

을 누르고, 공명을 일으키는 관의 길이값으로 부터 파장을 구하고 음속을 계산한다. 3번정도 반복하여 관의 공명위치를 주의깊게 관찰, 기록한다.

[참고] 필요하다면 정지되 있는 스코프윈도우, [그림5] 우측에 Voltage, ChA가 검은실선으로 선택된 상태에서 Transfer Data

을 누르면 Data영역의 Voltage, ChA 하단에 필요한 데이타로 저장되는 것을 볼 수 있다. 이를 File => Export Data => 데이터 선택하여 적당한 이름으로 저장하면 엑셀등으로 데이터를 처리할 수 있다.

(10) 소리주파수 1000Hz (전압진폭 2V) 에 대해서도 위의 과정을 반복하여 실험하고 공명이 일어나는 관의길이 데이터를 기록한다. 공명을 일으키는 관의 길이값으로 부터 파장을 구하고 음속을 계산한다.

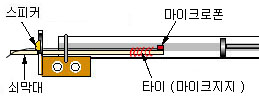
[그림13] 관 내부의 파형(음압)관찰

(11) 정상파가 일어나는 위치에서 관내부의 파형을 직접 관찰하려면 어떻게 해야할까? 마이크를 쇠막대 끝에 타이로 지지하고 마이크를 관 내부로 이동해가면서 파형을 관찰할수 있겠는가? 주파수 800Hz에 대해 n=1 인 공명위치에서 탐침막대 끝에 부드러운 철사로 감아 마이크를 고정하고 마이크를 조심스럽게 관 내부로 밀어넣으면서 위치에 따른 음압의 변화를 살펴보자. (이때 마이크가 최대한 수평을 유지하도록 자를 따라 조심스럽게 막대를 움직인다)

(12) n=3, 5 공명인 경우에 대해서도 위치의 변화에 따른 관 내부의 음압의 변화를 곡선으로 그릴수 있는가? 압력이 최대(또는 최소)인 지점은 파형의 어느부분에(배 또는 마디)에 해당하는가? 왜, 마이크가 초기위치(L=0)일때 압력이 최대 또는 최소가 되지 않는가? (이것은 관 끝에서 정확하게 배가 형성되지 않는다는 것을 의미한다.)

(13) 관 내부에서 마이크를 움직일때 음압이 최대(또는 최소)가 되는 지점사이의 거리, 즉, 파장을 직접 측정해서 관 끝 보정인자와는 상관없이 더욱 정확하게 음속을 계산해 보자. 당신은 관 끝 보정인자를 얼마로 잡을 것인가?

[주의] 실험이 다 끝난 후에는 내장 밧데리가 금방 소모되므로 반드시 핀 마이크를 꺼 놓는다.

[질문] 스피커 측의 관을 조금 열어 놓을때와 닫을때 공명길이가 달라지는 이유는 무엇 때문일까? 또, 열린관에 대해서 정상파 실험을 하려면 장비구성을 어떻게 해야 할까? 토의해 보자. (실험 여건상 우리는 열린관에 대한 실험을 하지 않는다.)

5. 참 고

(1) Waves on a string / Resonance Modes and the Speed of Sound (PDF 파일)

(2) 파형 구동자(Wave Driver)